[ベスト] 球 体積 表面積 公式 149827

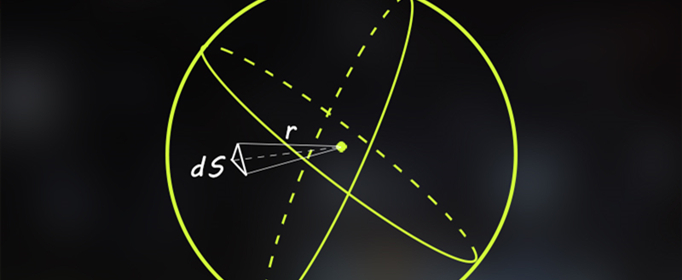
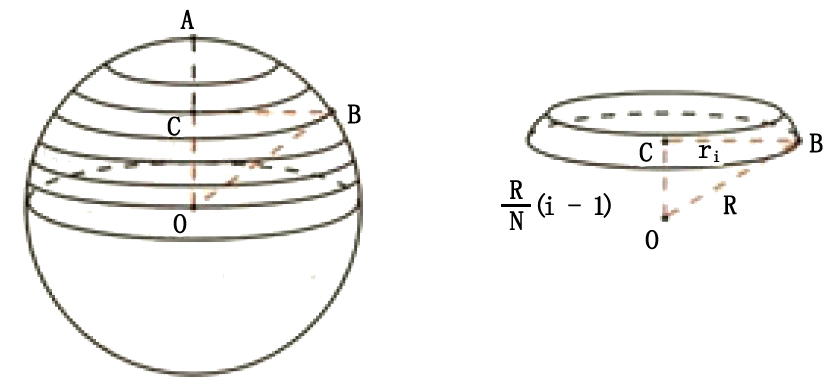
円と球の公式 \(D\)：直径 \(\rho\)：密度 円の面積 \(\left ( \displaystyle \frac {\pi}{4} \right ) D^2\) 円周 perimeter \(\pi D\) 円形度 circularity （等面積円の円周）／（周長） 球の表面積今回は中1で学習する「空間図形」の単元から 球の体積・表面積の求め方について解説していくよ！ 球というのは こういったボール状の形をしているものだよね！ 実は、ちょっとだけ公式が複雑だったりします (^^; 球の表面積公式の証明 (1) この証明は球の表面積を積分によって直接求める方法です。 図のような角度が θ θ から θΔθ θ Δ θ の青い部分の表面積を考える。 この図形を上から見ると円形になっている。 この円形の図形の半径は rcosθ r c o s θ となる

球体体积公式推导图解 万图壁纸网

球 体積 表面積 公式

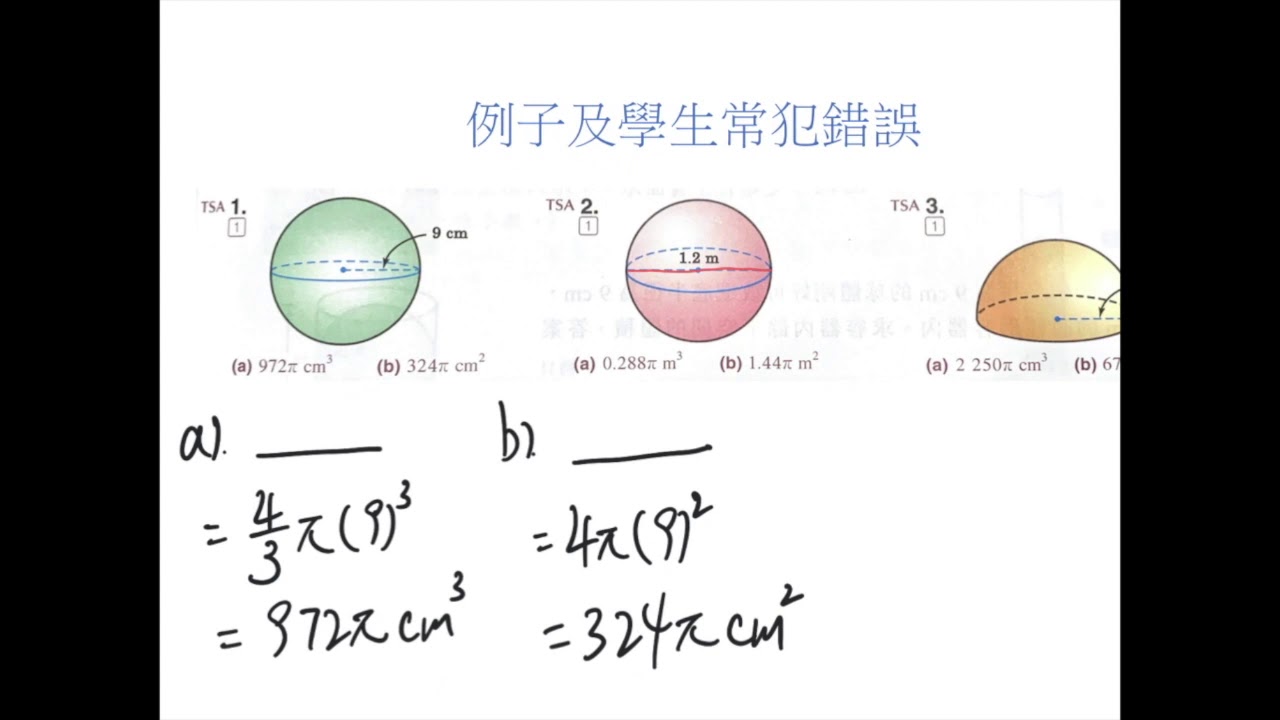
球 体積 表面積 公式-その体積は （「体積比は相似比の3乗比」を使えば，相似比が1：2だから体積比は1 3 ：2 3 =18 が求まる．） 球の表面積 半径 r の球の表面積を S で表わすと S=4πr 2 （解説） 底面積を S ，高さを h とするとき，三角錐，四角錐，･･･，円錐の体積は 体積と表面積の公式を書き出し、\(r\)（半径）の値を当てはめて計算しましょう。 解答 球の体積 \(\displaystyle V = \frac{4}{3} \pi r^3\)

椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com

 高校数学 kanrinin 微分でつなげる円や球の公式 今回の内容の動画版です→球の体積公式の微分が表面積になっている理由 円の面積、円周の長さおよび球の体積、表面積は次のように計算できます。球の体積と表面積にについて 1 はじめに 皆さん！どうして半径rの球の体積や表面積が（ πr 3 や4πr 2 になるのか不思議に思ったことはありませんか。ここで、一体誰がこのような結果にたどり着くような考え方をしたのかを、今から本を読んで知り得たことさて、今回は数学。「円」と「球」についてです。 これまでにいくつかの公式が登場してきましたね。 自信もって答えられますか？ 覚えていますか？ 円：小学校～ (円周)と(面積)の公式 球：中学校～ (表面積)と(体積)

円周の長さと円の面積は、小学校6年生で登場するが、球の計量は扱わない。球の表面積・体積が登場する のは、中学校1年生の 数学からである。いずれもその計量の公式 表面積 S＝4πr^2 ， 体積体積や面積を求めるとき、 公式が通用しないとき は 『 部分 』＋『 部分 』 『 全体 』－『 部分 』 を利用することはよくあります。 これはその典型です。 表面積は簡単には求まりませんが、部分部分は難しくはありません。 まずは半球の表面部分、 この円柱の側面積＝ 球の表面積の公式と同じ式をしていることが分かる． あなたは今、球の表面積を求める公式を知らないものとします． 円柱の側面積＝球の表面積 を示すことによって， （円柱の側面積＝ なので，） 球体の表面積＝ を示すことができます．

 球の体積と表面積の公式 半径 r r r の球の表面積は S = 4 π r 2 , S=4\pi r^2,\ S = 4 π r 2 , 球の体積は V = 4 3 π r 3 V=\dfrac{4}{3}\pi r^3 V = 3 4 π r 3 である。球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集 球の表面積の公式を使えば、半球の側面積（もとの球面の部分）は、 \begin{equation*} \frac{1}{2}\cdot 4\pi R^2=2 \pi R^2 \end{equation*} となるので、確かに球冠の面積の公式で求めた結果と一致しています。

球的体积和表面积公式怎么算球的表面积和体积 自媒体热点

球体体积公式推导图解 万图壁纸网

 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。 たとえば、半径30 cmのサッカーボールがあったとしよう。 こいつの体積は「4/3 × π × 半径の三乗」という公式をつかってやると、 ³ 4 3 × π × 30 × 30 × 30 = π c m ³ になるね。 これってサッカーボールの中にどれぐらい空気が入っているか球の体積の公式から、表面積Sは、 (4/3) π r 3 ＝ (1/3)・S・r より、S ＝ 4 π r 2 以上から、 （球の表面積） ＝ 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。 半球の表面積 S ＝球の表面積の半分＋半球の切り口である直径4cm（半径2cm）の円の面積であることから S = 4π × 22 × 1 2 ＋ 22π ＝ 8π ＋ 4π ＝ 12π 答え 12π cm² ～立体の体積・表面積を求める公式まとめ～ 立方体・直方体の体積の求め方 円柱の体積の求め

圆球体积公式 球的体积公式和表面积公式 徐州信息网

球冠体积 表面积在线计算器 大嘴狗在线计算器

V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin うさぎでもわかる解析 Part27 2重積分の応用（体積・曲面積の求め方） 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積（表面積）を求める方法についてまとめてい 球の体積をV、球の半径をr、円周率をπとしたとき、球の体積Vは以下の式で表すことができます。 V=4/3πr³ (球の体積の公式) 球の表面積の公式はS=4πr²

球體表面積及體積的推導 每日頭條

球体表面积公式 球体体积公式 环球信息网

 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず！ 球の表面積の公式を暗記するための語呂は、球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半 球の表面積の公式の覚え方・語呂合わせ 球の表面積の公式は 「心配アール二乗」 と覚えましょう。 ちなみに、球の体積の公式は「身の上心配アール三乗」でしたので合わせて覚えると良いです。 「どっちが表面積の公式で、どっちが体積の公式だっけ？

球表面積公式球體表面積 百度百科 Kmbymh

1

 球の表面積\(S(r)= 4\pi r^2\)から出発すれば、\(\int S(r)dr =4\pi \frac{1}{3} r^3 =\frac{4}{3}\pi r^3 =V(r)\)と球の体積が求められました。 以上が、円や球の公式の統一的な覚え方です。 n次元球の定義 n 次元球というのは n 次元の球です。 ちゃんと言うと、 n 次元空間内の「ある点」からの (ユークリッド)距離が「ある値」以下の空間を n 次元球と呼びます。 「ある点」を球の中心、「ある値」を球の半径と呼びます。 なお、今回は球の球の体積 球の体積 球の半径から体積と表面積を計算します。 一部が欠けた球の体積 一部が欠けた球の体積 一部が欠けた球の体積と表面積を計算します。 弓形の回転体の体積 弓形の回転体の体積 弓形の回転体の体積と底面積と表面積を計算します。

球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com

高中数学必修2教案 1 3 2 球的体积和表面积 淘文库

今回は 「球の体積や表面積」 について学習しよう。 球は2つの公式を覚えてしまえば、それでおしまい！ こんにちは。相城です。今回は球の表面積について書いていこうと思います。 中学生でも納得かな？なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。 ただし は幅 の部分の中央線である。 球の体積の求め方（公式）の次は、球の表面積の求め方（公式）を学習しましょう。 下の図のように、 半径rの球があるとき、球の表面積は、4πr 2 となります。

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張

球 球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球の表面積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは（ @t_kun_kamakiri ）。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り

球的表面积第1页 驾考预约大全

球表面積公式球體表面積 百度百科 Kmbymh

高中数学必修2教案 1 3 2 球的体积和表面积 淘文库

球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com

三棱锥体积公式 四棱台表面积公式 尚书坊

球的表面积公式和体积公式是什么 搜狗指南

球的体积 表面积 简书

球的表面積的求法 中學數學課 隨意窩xuite日誌

球体的表面积体积计算公式是什么 尚书坊

球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく

转载 球的体积表面积公式推导 孙网荣 新浪博客

球表面積公式球體表面積 百度百科 Kmbymh

積分球公式球的體積 Jvvx

椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

1

球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社

球體的體積與表面積 人人焦點

球的表面积推导带图 第1页 要无忧健康图库

圆球表面积 球体表面积的公式证明 篆体字转换器

球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典

半球表面积和体积公式 求半圆的体积公式和表面积公式 三人行教育网 Www 3rxing Org

球體表面積球體 表面積 體積 Vhjk

球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org

球體的體積與表面積 人人焦點

高中數學 空間幾何體的表面積和體積公式匯總及例題講解 人人焦點

球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com

球體體積 總表面面積 Youtube

表面积体积公式大全 万图壁纸网

圆球表面积公式推导球体的体积公式 表面积公式的推导

球缺 维基百科 自由的百科全书

012 球的体积空间几何体高中数学 Youtube

體表面積公式taiwanbio臺灣生技網 Hvamw

球體的體積與表面積 人人焦點

球体表面积公式 球体体积公式 环球信息网

数学一分钟球的体积公式推导证明 哔哩哔哩 つロ干杯 Bilibili

胶囊罐体 球冠高等于柱体半径 体积 表面积计算公式 三贝计算网 23bei Com

球体的表面积体积计算公式是什么 尚书坊

球的表面积第1页 驾考预约大全

球体体积与表面积公式有何巧妙的内在联系 哔哩哔哩 Bilibili

球の体積と表面積 Youtube

球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題

球面積計算球 Yxhsa

求球体的表面积和体积 修也 Csdn博客

球表面積計算球的體積 Jlxpis

球體的體積及表面面積 哔哩哔哩 Bilibili

積分球公式球的體積 Jvvx

球的體積求導便是球的表面積 互為逆運算 降維與升維 每日頭條

球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社

球体表面积公式 球体体积公式 环球信息网

積分球公式球的體積 Jvvx

球の表面積と体積の公式 数学fun

在球的体积公式中 为什么会出现三分之四这个奇怪的

简单几何体的表面积与体积 立体几何初步ppt 球的体积和表面积 下载 牛二ppt

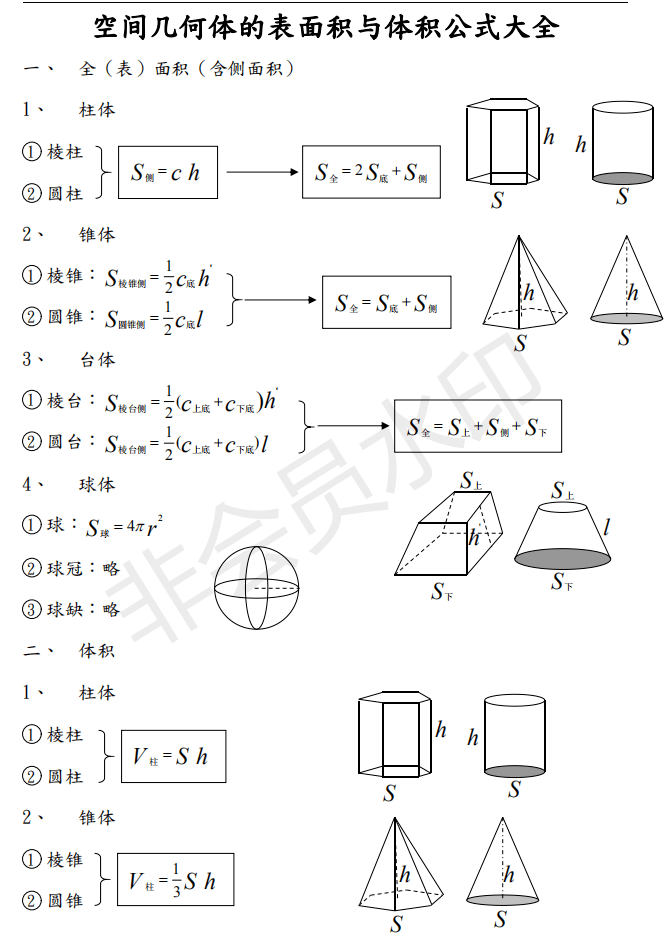
22高三数学第一轮复习 空间几何体的表面积与体积公式大全 升学 恒艾教育

中1 数学 6 5 球の体積 表面積 Youtube

球冠体积公式 球冠体积公式

球體體積計算公式球體體積公式 Hqgkiz

3

球的面積公式球體的表面積公式 Pxmode

球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客 球的体积公式推导过程

三棱锥表面积 四锥体表面积公式 尚书坊

球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org

球體積計算 Motics

各類幾何體的體積與表面積的計算問題 每日頭條

球的面積公式球體的表面積公式 Pxmode

球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科

球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学

球表面積計算球的體積 Jlxpis

球体体积公式 怎样计算球体的体积

球的体积公式和表面积公式 中国练字网

球面積計算球 Yxhsa

3

中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく

圓球體積計算圓球體的直徑40m 求此圓約1 4圓球表面積是多少 Jnkz

球體的體積球體 360百科翻譯此網頁 Gahzw

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网

用感覺理解球體表面積公式 Youtube

球缺体积和球冠表面积的计算公式及应用 晨起尘又落 Csdn博客 球缺的表面积计算公式

圆球表面积 球体表面积的公式证明 篆体字转换器

3 球的表面积和体积球的表面积公式是怎样推导出来的答 将圆球切成无 可爱图片库

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

球體積的前世今生 每日頭條

球体的表面积和体积的计算公式 星火网校

球体表面积公式 球体体积公式 环球信息网

球表面积公式推导图解 第1页 要无忧健康图库

球体表面积公式球体表面积球体表面积 公式证明 爱华网

面積公式微積14 4 Lhlv

球體體積 Athlet

圆环体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com

半球体积 表面积 截面积 球面积在线计算器 三贝计算网 23bei Com