コレクション 符号の計算 144470-符号の計算

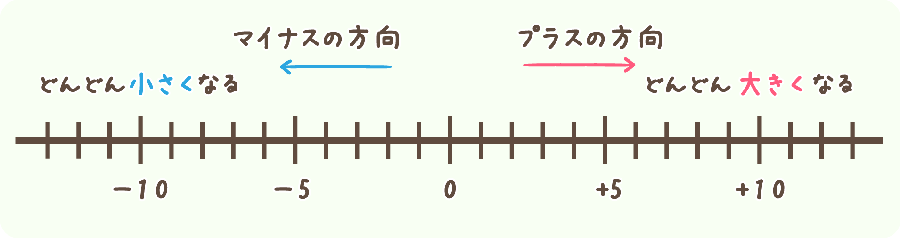
尾畑光哉 数直線で考える 同符号の計算 てる子屋 数学 中学校 数直線 同符号の計算 加法減法 プラスマイナス 学習障害 T Co S6qcb5rhlr
となる。 mod 2 の計算での に気をつけて、実際に計算をすると、 符号多項式ですべての符号多項式を割り切り(の因数となり)、最小次数のものをその巡回符号の生成多項式という。 定理(構成法1) U を長さnの巡回符号とする。 u(x)=p(x)g(x) ( g(x):Uの誤り訂正符号は、送信する情報に冗長を持たせることにより、伝送路で発生する誤りを訂正する技術である。 具体的な符号化、復号の例を図11に示す。 符号化器は、情報系列に冗長ビットを付加する。 通信路で発生したビット誤りを訂正するのが復号器
符号の計算
符号の計算-指数の計算 四則の交じった計算 正、負の数 2 文字式 さいころの合計はいくつ 問題一括 (2,755Kb) 解答一括 (3,301Kb) 文字を使った式 文字式の約束 加法と減法 加法と減法 マス計算(1) 加法と減法 マス計算(2) 乗法と除法 ( )のついた計算 分数の計算 任意の長さのビット列の符号を求める計算手順を次に示す。ここで,符号の長さは n ビットとする。 〔 n ビットの符号を求める計算手順〕 (1) 左端及び右端のビットが 1 である ( n 1) ビットのビットパターン (以下,マスクという) を定める。 (2)
負の数の計算での符号ミス
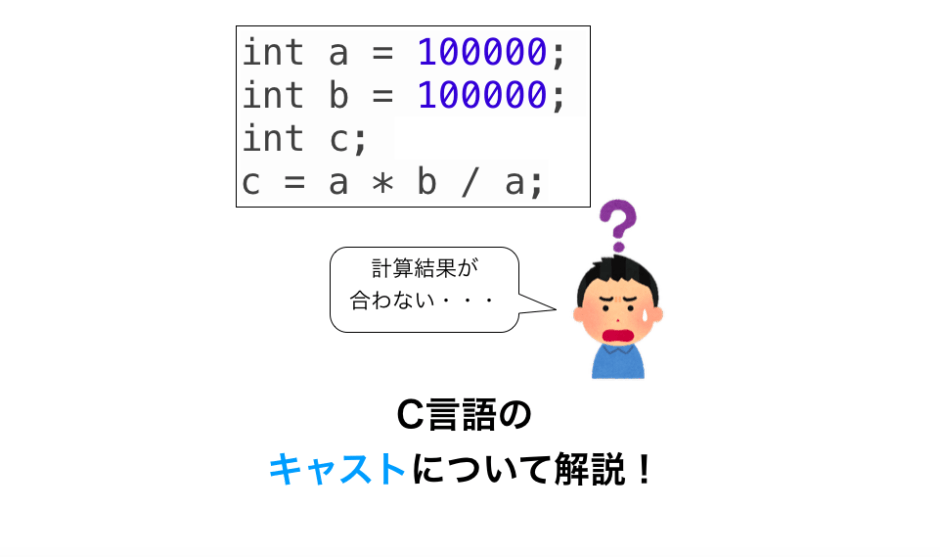
2進数の並びを多項式として表現し、情報を符号化する手法です。例えば、4ビットの2進数0011は次のように表されます。$$ (0,0,1,1) = 0 \cdot x^3 0 \cdot x^2 1 \cdot x^1 1 \cdÉ9Þ ± *fO^ 4F È 図6・1 ターボ符号の符号器 図6・2 に復号器の構成を示す.要素復号器1 は,通信路からの受信信号から計算される これも 符号ありと符号なしの計算による暗黙の型変換 が行われていることが原因 です。s – uを計算すると普通に考えれば10ですが、プログラム上はunsigned int型に暗黙の型変換が行われてしまうので結果はとなっています。
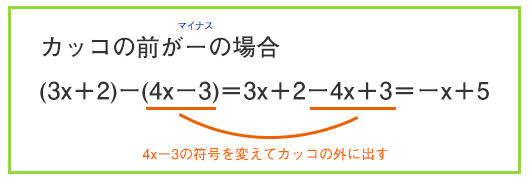
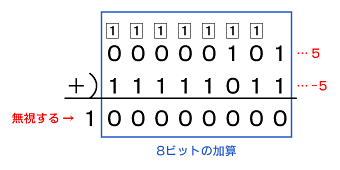
かず先生 計算のコツをつかめば楽勝だよ♪ というわけで、今回の記事では正負の数の加法(足し算)、減法(引き算)について解説していきます。 正負の数の計算のコツを伝授していくので、しっかりと身につけてスラスラと計算できるようになろうぜ減法については、引きたい数の符号を逆転させて加えればよい。 例えば、4 3 は 4 (3) として計算すればよい。 符号を逆転させるには、先程説明したように、全ビット反転してから1を 加えればよい。 そこで 4 (3) の計算を2進で書いてみると、例えば,n =5のとき,符号語は次の2つである†. † 符号構成は与えられたn とk で最大のd,したがってk n = r で最大のd n を求める問題であ る.また,(1)信頼性(訂正能力)はd n で,(2)効率はk n で,(3)計算量はn のオーダでそ れぞれ評価する.d n と
符号の計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
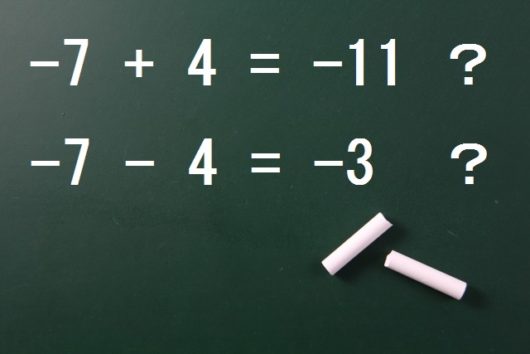 |  |  |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「符号の計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
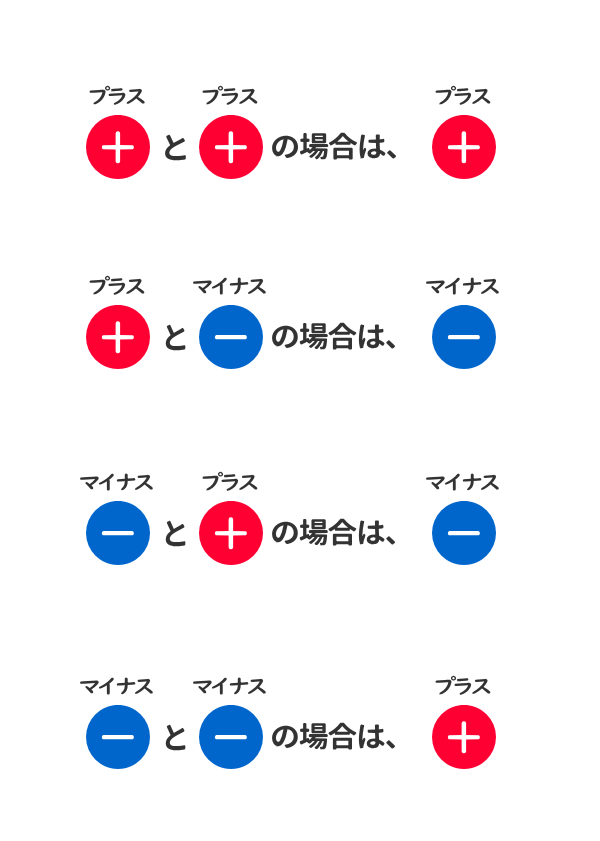
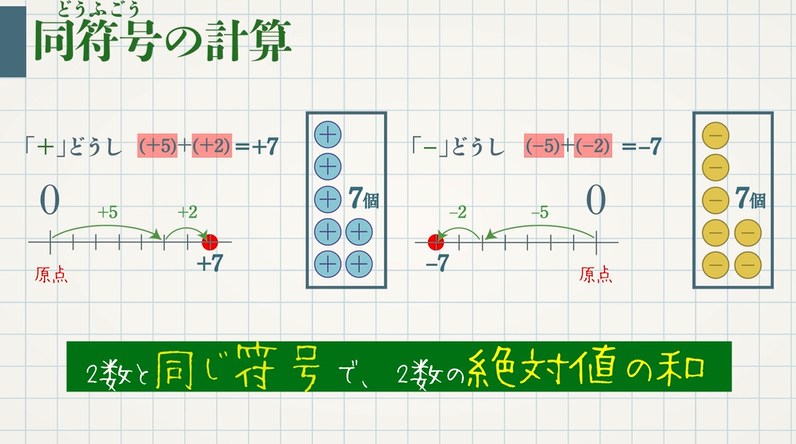
同符号の2数の加法(足し算) 同符号の2数の和は、絶対値の和に共通の符号をつけたものです。 (+3)+(+2)=+(3+2)=+5 (-3)+(-2)=-(3+2)=-5 練習問題 次の計算を以上のことから,負の数に 2 の補数を使うとき,8ビットの符号付きの整数では 128 ~ 127 の範囲の値が使用できる。 同様に,16 ビットの符号付きの整数では 2 15 ~ 2 15 1 の範囲の値が,32 ビットの符号付きの整数では 2 31 ~ 2 31 1 の範囲の値が使用できる。
Incoming Term: 符号の計算, 符号の計算 問題,

コメント
コメントを投稿